Some variations of Recamán's Sequence
Inspired by Alex Bellos, who presented clever illustration of Recamán's Sequence in recent video from Numberphile, I decided to implement this sequence in MATLAB/GNU Octave enviroment and get some other views of this sequence. And, what is the most important - get much more terms and see how they looks like.
The general idea of Recamán's Sequence is substracting the present index of the sequence from previous term every time we can do this so the result is over than zero. And second condition: the result have to be new term in the sequence, terms cannot be repeated. In other cases we define new term by adding present index, not substracting. Let’s see how it looks like in math expression:
As you can see, it is not difficult to express. Using this formulas, we can generate the Recamán's Sequence, and its first few terms are: 0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, …
On first sight, it is hard to see something alluring in this sequence. Just some numbers. But the beauty of mathematics lies in expressing apparent universality in many ways. Some of them are very interesting. Like this one. Let’s draw some graphs.

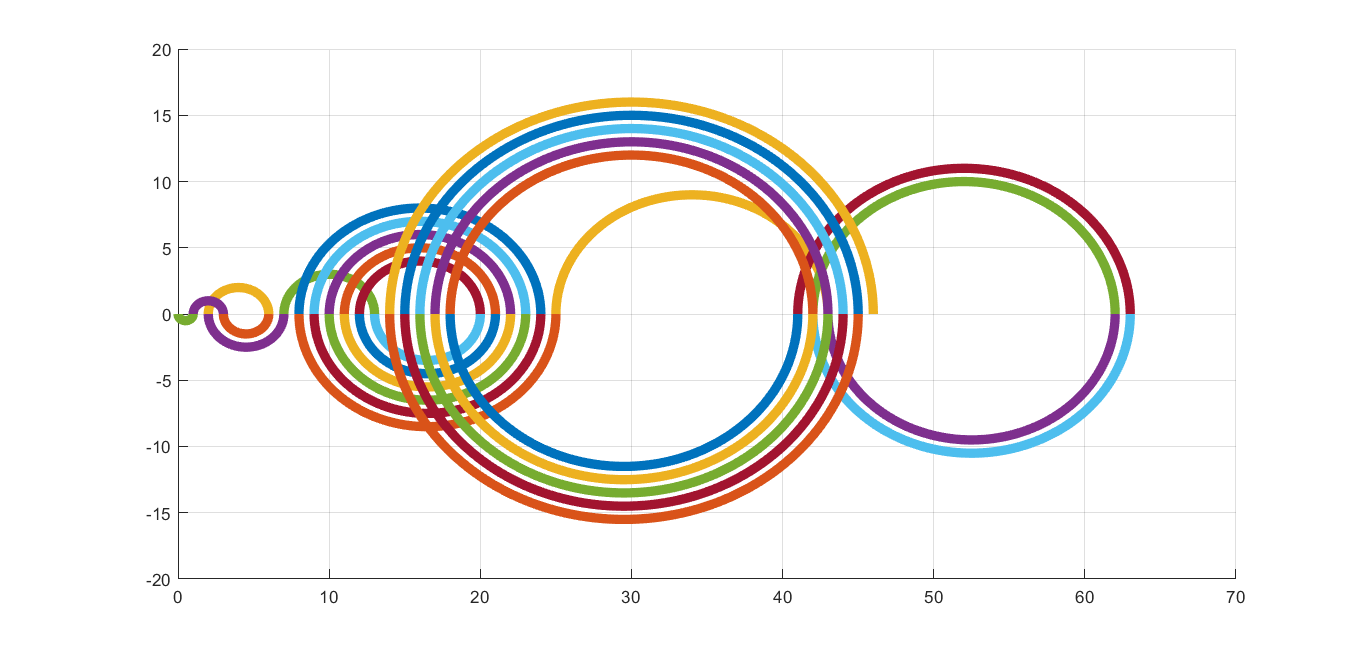
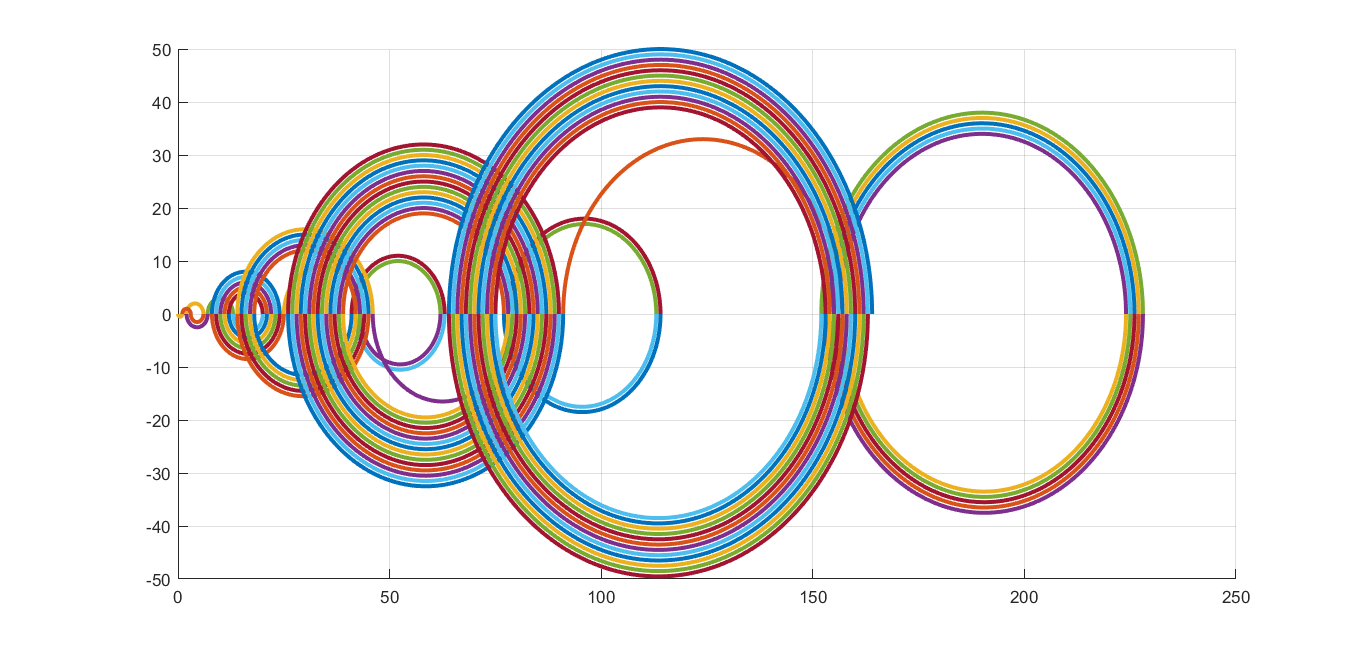
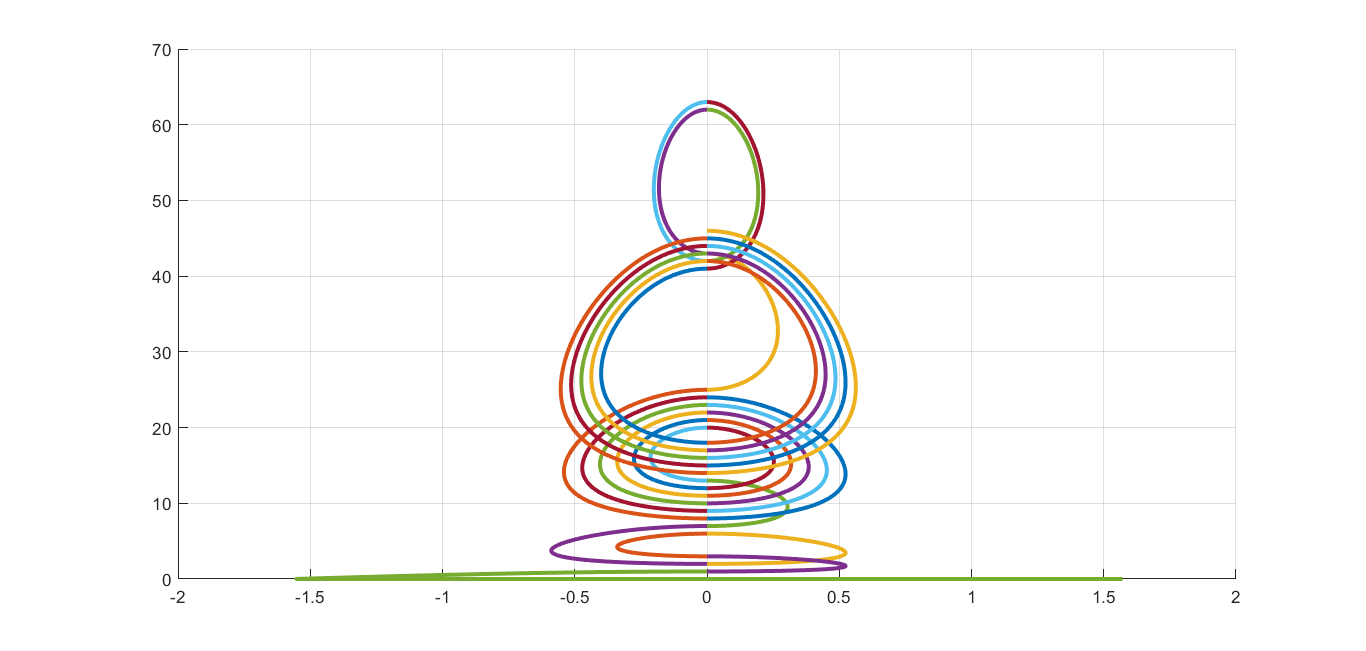
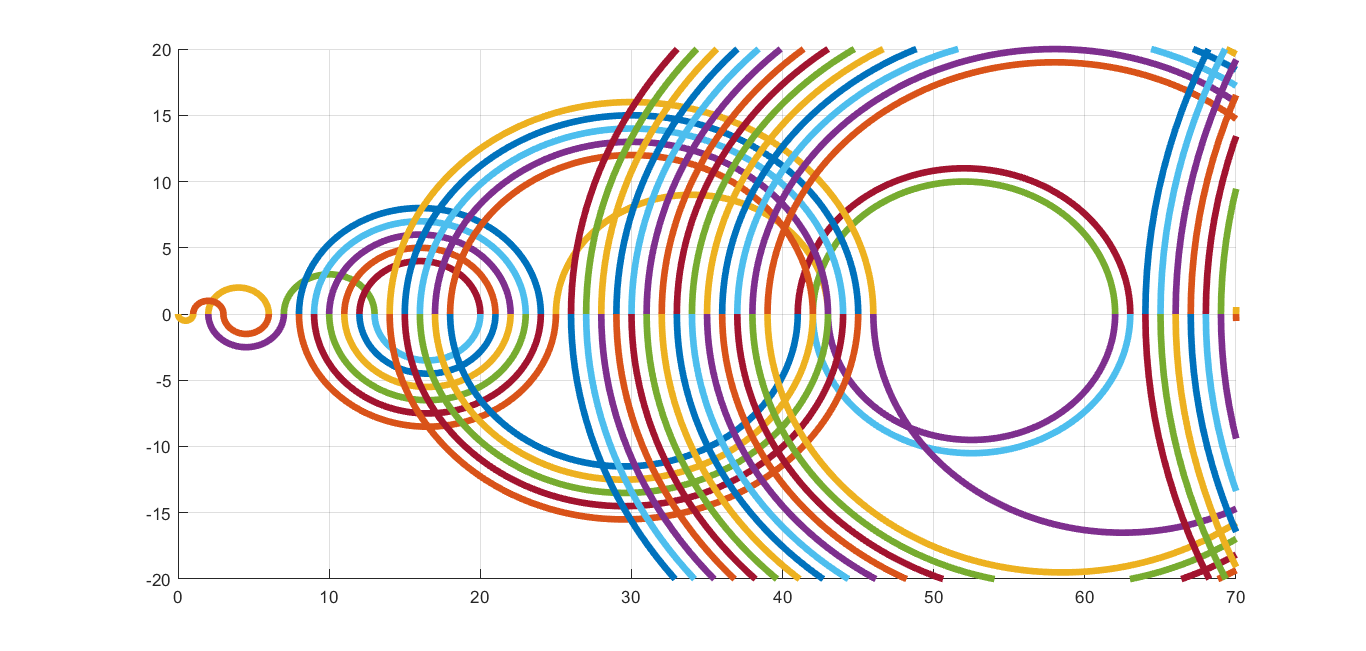
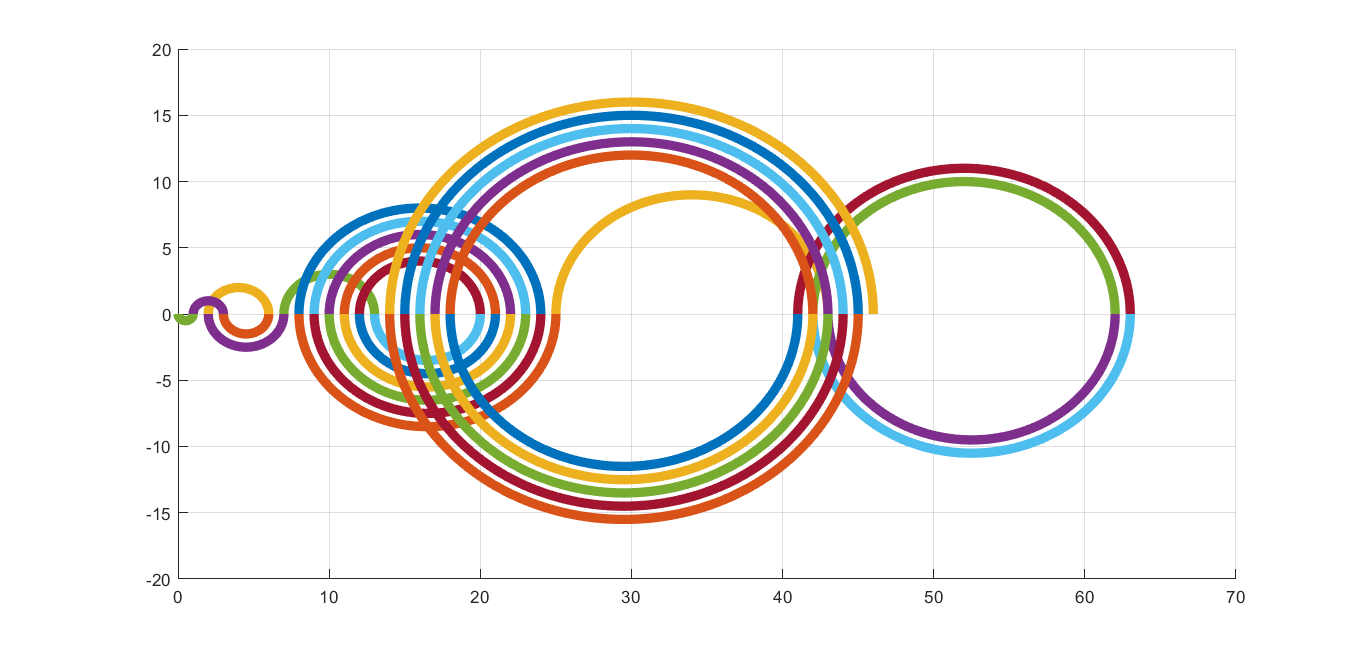
If we use semicircles to link neighboring terms of the sequence and we assume that we change angle from 0 to π and from π to 2π alternately, we can get such pictures. Radius of each circle is of course related to terms and it is present term minus previous term divided by 2.
As we can see, in maths we can find the element of beauty.
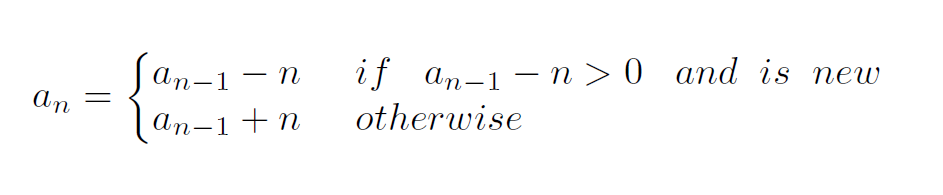







Comments