Lament matematyka Paula Lockharta to opowieść o tym jak zepsuto nauczanie matematyki w szkołach i być może zapowiedź tego samego dla innych przedmiotów. Autor zaczyna swój wywód od porównania matematyki do muzyki. Jedna i druga dziedzina posiada swój unikalny język – w muzyce jest to zapis nutowy. Koszmar, z którego budzi się bohater opowiadania, zaczyna się od niewinnego uczynienia muzyki obowiązkową, a kończy… wąchaniem własnych pierdów przez protoplastów tego zamieszania. Zaprzęgnięto pedagogów, uruchomiono machinę systemu szkolnictwa i państwa do uregulowania podstawy programowej. Z czasem doprowadziło to do tego, że dzieciom w szkołach nakazywano starannie pisać nuty, jednocześnie pozbawiając ich praktycznej strony muzyki – usłyszenia tych nut.

To bardzo dużo ciężkiej pracy, ale później w liceum i na studiach uczniowie to docenią, kiedy wreszcie będą mogli usłyszeć to wszystko

Oczywiście nie każdy idzie do liceum, nie każdy idzie na studia muzyczne. A więc gro osób pójdzie dalej w świat z nabytą niechęcią do muzyki (matematyki), nie wiedząc nawet co robiło przez lata nauki szkolnej, ani do czego to było potrzebne.

Równocześnie, gdzieś na drugim końcu miasta, z podobnego koszmaru budzi się z ulgą malarz… Ku swojemu zaskoczeniu znalazłem się nagle w zwykłej szkolnej klasie. Nie było sztalug, tub z farbami – nic z tych rzeczy. „Och, nie używamy farb aż do liceum” – usłyszałem od uczniów. „W siódmej klasie głównie poznajemy kolory i narzędzia do ich nakładania.

Dalej nauczyciel tego pseudo-malarstwa przyznaje z dumą, że sam nigdy niczego nie namalował na czystym płótnie. Posługiwał się jedynie zestawami dydaktycznymi przygotowanymi dla nauczycieli. O ile malarstwo i muzyka oparły się tej smutnej wizji dydaktycznej – bo w tych dziedzinach jeszcze słucha się najbardziej zainteresowanych, czyli uczniów – o tyle matematyka akurat nie podołała. Matematyka jest nauką, w której nie brak harmonii, symetrii, regularności. Posługując się czystą arytmetyką i algebrą, jedynie nieliczni są w stanie zauważyć analogie i ucieszyć się nimi. W pozostałych uczniach zostaje zniszczona naturalna ciekawość. Strzępy geometrii i stereometrii (które działają na wyobraźnię) rzucone jak ochłapy na końcu podręcznika pod koniec roku szkolnego to kpina.

Nasze społeczeństwo jest całkiem hojne w uznawaniu artystycznego statusu: artystami są architekci, szefowie kuchni, nawet telewizyjni reżyserzy. Dlaczego nie matematycy? Część problemu bierze się stąd, że nikt nie ma bladego pojęcia, czym matematycy się zajmują.

W dalszej części Lamentu Autor uzasadnia tezę, że matematyka jest sztuką. Bo w zasadzie dlaczego miałaby nie być? Ostatnie zdanie z przytoczonego cytatu tłumaczy większość przypadków nie zrozumienia tego stanu rzeczy. W naszej kulturze matematyk to ktoś o ścisłym umyśle; już samo słowo „ścisły” narzuca pewne więzy jakoby miało ograniczać jakąś przestrzeń myślenia/poruszania się. Kto dziś nie jest artystą? Mam wrażenie, że to określenie bardzo spowszedniało i przy jakiejkolwiek krytyce artystów lepiej ugryźć się w język, bo może się okazać, że czyjeś wrażliwe ego nieopodal zostało dotknięte. I nie piszę tego jako przedstawiciel matematyków, bo matematykiem nie jestem. Jako obserwator chcę tylko zwrócić uwagę na pewne zjawisko, które sam niedawno dostrzegłem. Dalej Autor pisze, że

nie istnieje nic bardziej poetyckiego, nic bardziej marzycielskiego, nic tak radykalnego, wywrotowego, psychodelicznego, niż matematyka. Matematyka jest tak oszałamiająca jak kosmologia, czy fizyka (matematycy wymyślili czarne dziury na długo zanim astronomowie zdołali je w rzeczywistości odnaleźć) – i pozwala na większą swobodę ekspresji niż poezja, sztuki plastyczne i muzyka (które bardzo mocno zależą od własności fizycznego świata). Matematyka jest najczystszą z nauk i równocześnie najbardziej niezrozumianą.

Matematyka obiera sobie za cel prostotę. A przecież najbardziej elementarne obiekty nie istnieją, operujemy nimi w wyobraźni, na kartce papieru. Odcinek, który jest prostą kreską na kartce, w rzeczywistości mógłby być np. kawałkiem pręta, liny, deski. Wszystkie te obiekty są niedoskonałe, składają się ze skończonej liczby chaotycznie wibrujących atomów. To nie jest wystarczająco proste i piękne, żeby znalazło swoje miejsce w matematyce. Odcinek ma być doskonały.

Autor podaje przykład trójkąta wpisanego w prostokątną ramkę. Ciekawym spostrzeżeniem jest to, że obiekty matematyczne mówią; mają jakieś niezależne od nas informacje. Trójkąt wpisany w ramkę zajmuje określone pole powierzchni prostokąta. Nie wiemy jakie to pole, możemy jedynie spróbować się dowiedzieć, ale nie mamy wpływu na jego wartość. Ciężko też zmierzyć to pole jakimiś przyrządami, skoro pracujemy na przedmiocie wyimaginowanym. Aby badać wyimaginowane obiekty trzeba bezwzględnie użyć imaginacji.
…no chyba, że ukończyło się kilka klas szkoły powszechnej. Wtedy wiadomo, że wzór na pole trójkąta to P = ½ah i problem jest rozwiązany – trójkąt zajmuje połowę powierzchni prostokąta. W przeciwnym wypadku, rysując wysokość trójkąta, można zauważyć, że taka sama część trójkąta jest po jednej i po drugiej stronie jego ramion. Zatem można wydedukować, że to idealnie połowa prostokąta. Poruszanie się po matematyce zostało sprowadzone do podążania utartymi schematami i do umiejętności korzystania z wzorów wziętych z kosmosu. To tak jakby szczytem malarstwa nazwać popularne teraz malowanie po numerach – obrazek, który zawiera pola z podpowiedzią jakim kolorem mamy je pokolorować.

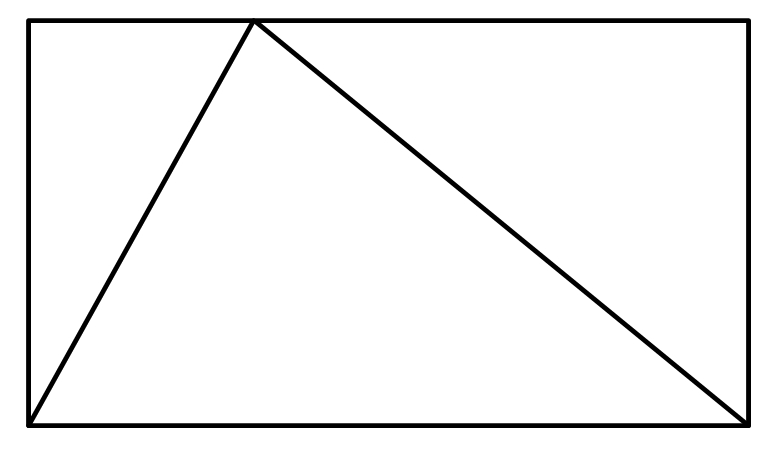
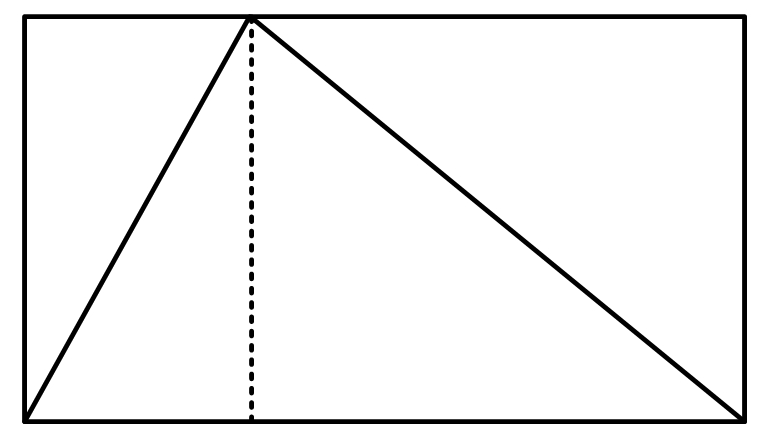
Korzystanie z księgi wzorów ogranicza twórcze myślenie w celu rozwiązania jakiegoś problemu. Ogranicza także ilość błędów popełnianych przez uczniów – i pewnie dlatego te wzory kładzie się im do głów. W szkole uczą nas, że błąd jest zły i to jest problem. Błąd jest dobry, bo przybliża nas do prawdy. A frustracja z popełnionego błędu może zrodzić kolejne nowatorskie pomysły, rozwiązania.

W dalszej części Autor podejmuje problem uprawiania matematyki. Stawia tezę, że obecność matematyki w szkole argumentuje się jej powszechnością, przydatnością itp. Jawi się ona jako narzędzie do nauki, do tworzenia technologii, jako pomoc dla inżyniera. Natomiast matematykę – podobnie jak poezję czy muzykę – tworzy się dla czystej radości tworzenia i odbioru, dla rozwijania i uszlachetniania ludzkiej duchowości. Ciężko byłoby inaczej uzasadnić kierunki, które obrali matematycy na przestrzeni wieków: czy to Euklides w starożytności, czy Riemann w czasach współczesnych. Obydwaj zajmowali się wysoce abstrakcyjnymi tematami, a wiele z zaobserwowanych zależności, które sformułowali, nie ma zastosowania w żadnych urządzeniach, maszynach czy konstrukcjach.

Sugeruję tylko, że fakt istnienia, przypadkiem, praktycznych zastosowań matematyki, nie oznacza jeszcze, że ona na tym właśnie polega. Muzycznymi utworami da się prowadzić armie do boju, ale to nie jest powód, dla którego ludzie piszą symfonie. Michał Anioł udekorował pewnego razu pewne sklepienie, ale założę się, że miał na myśli coś nieco bardziej wzniosłego niż pomalowanie sufitu.

Dalej Autor sugeruje, że matematyka została dawno usunięta z programów nauczania, a przedmiot funkcjonujący pod tą nazwą to wydmuszka. Trudno się nie zgodzić, w większości przypadków mamy do czynienia z karykaturą matematyki. Osobiście przyznam, że w szkole średniej trafiłem na znakomitego nauczyciela matematyki, niestety już świętej pamięci. Starszy pan, który ekscytował się nawet drobnym dowodem wyprowadzonym na poczekaniu na tablicy. W jego oczach dało się zobaczyć dziecięcą radość z uprawiania tej dziedziny nauki. Animuszu dodawał fakt, że ów nauczyciel miał liczne sukcesy w matematyce i zrezygnował z pracy na uczelni wyższej, został z młodzieżą szkół średnich. Szkoda, że takich nauczycieli jest tak niewielu.

Zdjęcia:
[1] — Jeswin Thomas, Unsplash