Czytając kolejny archiwalny numer czasopisma Matematyka-Społeczeństwo-Nauczanie natknąłem się na ciekawy sposób na obliczenie pola dwunastokąta foremnego wpisanego w okrąg. Cały artykuł, napisany przez czeskiego profesora w 1991 roku, odnosił się do ówczesnego stanu wiedzy studentów matematyki. I jak sam profesor František Kuřina wspomina — nie było się czym chwalić:

Chciałbym dać teraz parę przykładów, jak bardzo niski poziom kultury matematycznej reprezentują moi studenci, przyszli nauczyciele.

Przytoczę jeszcze fragment artykułu definiujący kulturę matematyczną:

Moim zdaniem następujące składniki kultury matematycznej są niezbędne dla pomyślnej pracy nauczyciela:

1. Zdobycie sprawności matematycznej.
2. Zrozumienie ciągłego przejścia w poszczególnych dyscyplinach matematyki między matematyką — nauką i matematyką — przedmiotem nauczania.
3. Zrozumienie języka matematyki.
4. Umiejętność wybierania odpowiednich metod przy rozwiązywaniu zadań.
5. Posiadanie dobrej wyobraźni geometrycznej.
6. Opanowanie techniki obliczeń.
7. Opanowanie umiejętności przeprowadzania dowodów.
8. Opanowanie umiejętności wprowadzania pojęć.
9. Możliwość uprawiania w pewnym stopniu twórczości matematycznej.
10. Postrzeganie piękna matematyki.

Jednym z przykładów, które autor artykułu zadał swoim studentom było wyprowadzenie wzoru na pole dwunastokąta foremnego wpisanego w okrąg. Poprawnych odpowiedzi pojawiło się bardzo dużo, zadanie stosunkowo proste było polem nie tylko do sprawdzenia poprawności rozwiązania, ale także do sprawdzenia sprytu, spostrzegawczości i wyobraźni studentów. Pojawiły się prawidłowe rozwiązania, które wyglądały jak nic nie znaczące szlaczki. Autorów takich rozwiązań ciężko posądzać o wypełnienie 10-tego punktu powyższej listy. Ale pojawiły się także rozwiązania o nieco bardziej zgrabnym kształcie. Nie będę tych rozwiązań przytaczał. Tak jak wspomniałem — dróg było wiele, studenci korzystali z twierdzenia Pitagorasa, twierdzenia sinusów, twierdzenia kosinusów, wzoru Herona itp.

Profesor František Kuřina przytacza bodajże najprostsze rozwiązanie, które wymagało zauważenia, że wysokość każdego z 12 trójkątów opuszczona na bok o długości promienia koła opisanego na tej figurze, równa jest połowie tego promienia. Mamy zatem proste działanie:

Kolejnym rozwiązaniem, które było wysoce pożądane było rozwiązanie pochodzące z III wieku. Autorem jest Chińczyk, którego godności niestety nie znamy. Kluczem dojścia do wyniku 3r² jest dostrzeżenie, że ćwiartkę dwunastokąta można podzielić na 3 równoboczne i 6 równoramiennych trójkątów, które stanowią dopełnienie pozostałych ćwiartek do kwadratów o boku r. A wzór na pole kwadratu zna każdy z nas.
Kwadratów jest 3, więc wynik gotowy — 3r².

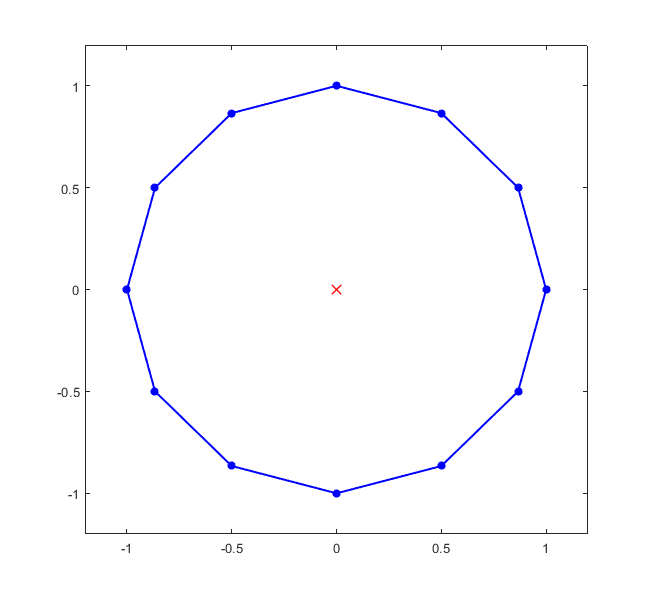
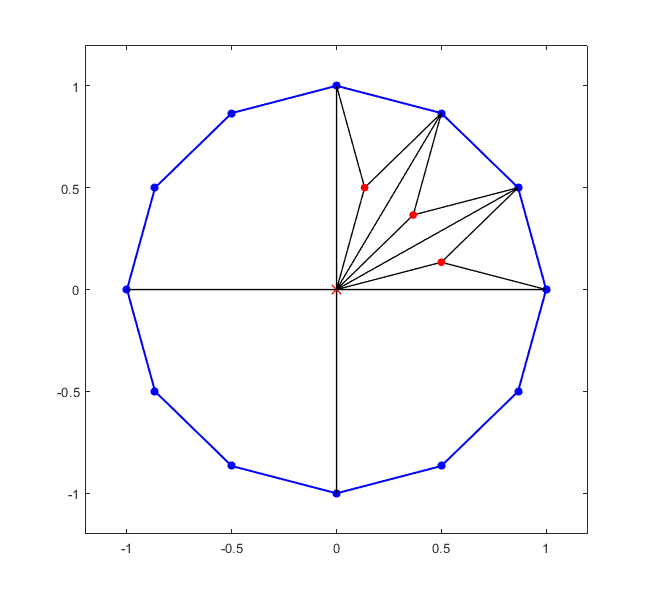
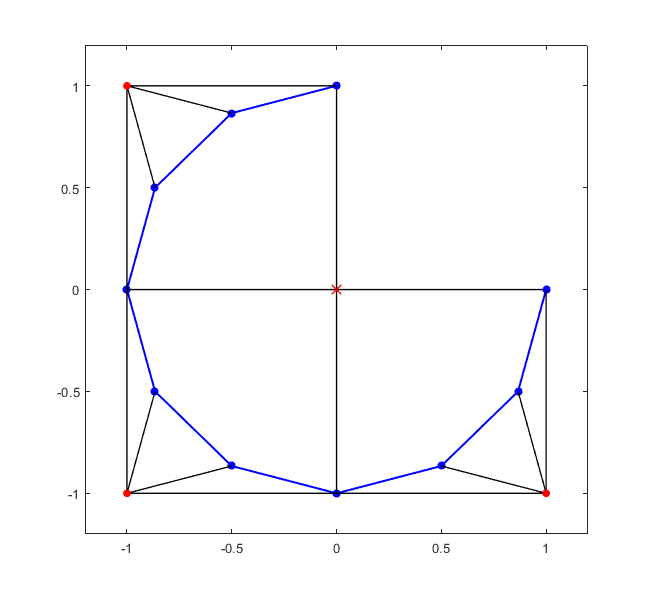
Temu rozwiązaniu nie można odmówić elegancji i piękna. Chińszczyzna w matematycznej kuchni okazuje się być chińszczyzną o niezwykle wyrafinowanym guście. Smacznego!

Źródło:
[1] Kuřina F. — Kultura matematyczna nauczyciela matematyki, Matematyka Społeczeństwo Nauczanie 1/1991.

Grafiki wygenerowane w Matlabie