Po przeczytaniu Lamentu Lockharta – część II
Are you sure you want to move this PROGRAM MATEMATYKI to the Recycle Bin?
W dalszej części Lamentu Paul Lockhart stwierdza wprost, że programu matematyki nie należy poprawiać, należy go wyrzucić.
Cała ta wrzawa i całe to przystrajanie się w nowe piórka, deliberacje, które „zagadnienia” przedstawiać i w jakim porządku, czy używać tej notacji, czy może tamtej, albo jakiego modelu kalkulatora używać – wszystko to jest jak przestawianie krzeseł na górnym pokładzie Titanica, na miłość Boską! Matematyka jest muzyką rozumu.
Trudno się nie zgodzić. Sam pamiętam jak nauczyciele niejednokrotnie odwoływali się do podstawy programowej. Oczywiście zawsze w jednej z dwóch sytuacji: albo uzasadniając konieczność realizacji danego materiału (częstokroć nudnego) albo uzasadniając brak realizacji danego materiału (często tego ciekawszego). Wszystko sprowadzało się w zasadzie do stwierdzenia, że to co jest w podstawie programowej może być na egzaminie/maturze/etc. Dlatego tym bardziej cieszy mnie fakt, że miałem przyjemność być pod opieką mojego nauczyciela matematyki z liceum; przemycił nam wiele treści spoza tej mitycznej podstawy programowej, np. liczby zespolone. Nawiasem mówiąc, liczby zespolone są abstrakcją samą w sobie i jest w nich coś – jak pisze Autor w cytowanym fragmencie z poprzedniego wpisu – psychodelicznego. Jednostka urojona, pośród tylu ścisłych i zwartych pojęć w matematyce, wygląda niemal jak obraz Salvadora Dali zestawiony z dziełami barokowych mistrzów pędzla.

Wszystkie te żałosne próby, by matematykę zaprezentować jako użyteczną w codziennych problemach, są nieuchronnie wymuszone i sztuczne: „Otóż, dzieci, gdybyście znały algebrę, mogłybyście dowiedzieć się, w jakim wieku jest Maria, wiedząc, że ma o dwa lata więcej niż dwa razy tyle, ile miała siedem lat temu!” (Zupełnie jakby komukolwiek zdarzyło się dysponować tak idiotycznie skleconą informacją zamiast po prostu wiekiem Marii.)
Ach! To słynne zadanie z obliczaniem kto ile ma lat. Wszyscy doskonale wiemy jak przydatne w życiu są takie zadania. Z jednej strony program nauczania jest wydęty od zadań uzasadniających przydatność matematyki w codziennym życiu, a z drugiej strony serwuje się uczniom zadania jak to powyżej. Czemu nie pokazać innych stron matematyki, nie wkładając jej na siłę w formę „użyteczność”? Autor stwierdza, że wspaniałość tej dziedziny polega na absolutnym braku związku z codziennością. Matematyką można się bawić, wiele by nie straciła ze swego uroku gdyby potraktować ją jak sztukę cyrkową. Zamiast mnożyć zadania mające wyrobić nawyk mechanicznego podchodzenia do problemu na egzaminie, można by potraktować tę dziedzinę jako okazję do rozmyślań, rozwiązywania zagadek, np.
Przypuśćmy, że znamy sumę i różnicę dwóch liczb. Czy w jakiś sposób mogę się dowiedzieć, co to są za liczby?
Jeśli ktoś ma ochotę na zabawę to proszę podać sposób rozwiązania tego problemu w komentarzach lub jako ripostę. Dodam jeszcze pewne ograniczenie: jak ktoś rozwiąże to zadanie jednym sposobem i opublikuje, to kolejna osoba musi znaleźć inny sposób, inną drogę. Dowodów na twierdzenie Pitagorasa jest lekko ponad 100, więc myślę, że dróg do rozwiązania tego zadania nie braknie :).
Jabłka są czerwone, jabłka trzeba jeść…
…Siedem razy osiem jest pięćdziesiąt sześć. Kolejnym problemem, który dostrzega Autor Lamentu jest uczynienie matematyki przyjazną, cukierkową. No bo jak już się uczy tak znienawidzonego przedmiotu to przynajmniej nie powinno się dokładać dzieciom koszmarów. Paul Lockhart przytacza historyjkę o Panu Obwodzie, który otacza Panią Pole. My także znamy wiele wierszyków – jak ten o jabłkach, które trzeba jeść. Jest to oczywiście droga na skróty. Po co opowiadać uczniom o historii, która doprowadziła do znalezienia wzoru na pole i obwód koła? O tajemniczej i genialnej liczbie π? Ciężko znaleźć inny przedmiot, który ogołaca się z jego własnej historii. No może poza WF-em. Ale żeby na geografii nie wspomnieć o historii i biologii? Albo na języku polskim pominąć historię, filozofię? Nie wspomnę już o omawianiu bieżących dla danej dziedziny wydarzeń.
Jaka jest przekątna sześcianu? Czy liczby pierwsze ciągną się w nieskończoność? Czy nieskończoność jest liczbą? Na ile sposobów da się symetrycznie pokryć płaszczyznę? Historię matematyki wypełniają zagadnienia raczej tego rodzaju, a nie wzory i algorytmy wyrzygiwane przez nauczyciela w nieskończonym potoku wraz z ćwiczeniami zaprojektowanymi wyłącznie po to, by z algorytmów dało się w ogóle skorzystać.
Nikt nie lubi jak przerywa mu się zabawę w trakcie. Gdyby lekcja matematyki wyglądała jak poligon łamigłówek, to nauczyciel nie miał by wiele do roboty. Musiałby jedynie cierpliwie czekać, aż uczniowie zaczną jęczeć z bólu i wtedy podać drobną podpowiedź. Łatwo powiedzieć – wiem. Lekcja ma 45 minut i nauczyciele też – jak już wcześniej wspomniałem – mają realizować zadany program. Na łamigłówki może być czas na kółku matematycznym. Mój nauczyciel matematyki z liceum wiele razy powtarzał, że on sam trenuje codziennie. Że jego wiedza nie bierze się znikąd. Jednakże nigdy nie zadawał zadania domowego typu: „zróbcie przykłady od 1 do 50, nieparzyste numery, to będzie na klasówce”. Na lekcjach rozwiązywaliśmy kilka przykładów i do domu było kilka przykładów. Myślę, że sukcesem było powtórzenie w domu tego zadania z lekcji, a prawdziwym tryumfem rozwiązanie nowego przykładu.
Nikt nie marnuje czasu na lekturę podręczników na warsztatach malarstwa, nikt nie ćwiczy w nieskończoność malarskich technik. Robi się po prostu to, co naturalne – dzieci najzwyczajniej malują. Nauczyciel zaś chodzi pomiędzy sztalugami, rzucając sugestie i czasem wskazówki.
Dalej Paul Lockhart zauważa jeszcze jedną przyczynę takiego stanu rzeczy w nauczeniu matematyki. Przez lata nauczania pseudo-matematyki wytworzyła się pewna zależność pomiędzy wydawcami podręczników, a nauczycielami. Nie znam genezy tego problemu, ale istnieje pewna podaż ze strony wydawców podręczników, a nauczyciele generują popyt na takie, a nie inne treści w tych podręcznikach i pomocach naukowych. W pewnym sensie jest to zamknięte koło. Na szczęście są inne, alternatywne wydawnictwa (jak np. Szkoły Matematyki Poglądowej organizowane 2 razy do roku w formie konferencji, zbiór artykułów jest następnie wydawany w formie papierowej), które traktują o istocie matematyki, pomijając tą jej część, której już wszyscy mamy dość.

Z Polski pochodzi wielu sławnych i znanych matematyków (Banach, Ulam, Kac, Stark, Sierpiński, Borsuk i inni). Myślę, że nauczanie matematyki wiele by zyskało, gdybyśmy uczyli takiego podejścia jakie mieli nasi mistrzowie w tej dziedzinie. A jak oni zabierali się do matematyki? Przesiadywali w kawiarni szkockiej we Lwowie w otoczeniu dymu tytoniowego i oparach wysokoprocentowego alkoholu. Na stoliku notowali swoje twierdzenia i dowody matematyczne, które po zamknięciu lokalu poddawały się zwilżonej ścierce. Rzucali sobie nawzajem wyzwania, startowali w zdrowej rywalizacji. Bawili się tym. I tacy ludzie są teraz w panteonie polskich matematyków. Oczywiście zabawy powinny być proporcjonalne do wieku – nikt by przecież nie organizował melanży alkoholowych dla uczniów szkół podstawowych. Myślę, że jednak istota problemu jest jasna – schematyczna matematyka versus matematyka niekonwencjonalna.
Zdjęcia:
[1] — mem własnej roboty
[2] — wu yi, Unsplash
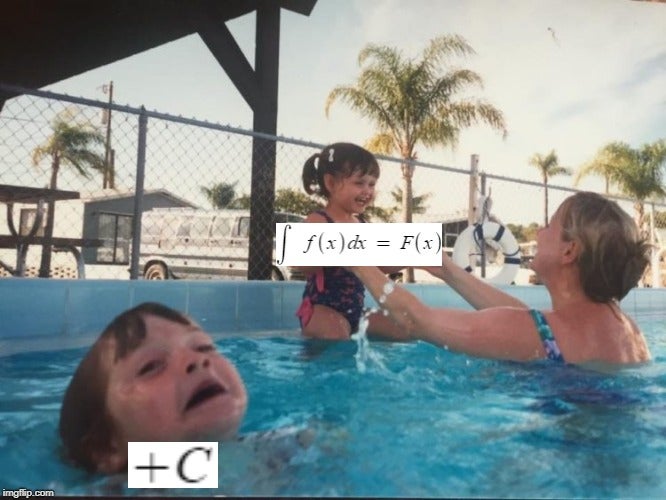





Comments